Sparkle IconBeyond Accuracy: Dissecting Mathematical Reasoning for LLMs Under Reinforcement Learning

Jiayu Wang1, Yifei Ming2, Zixuan Ke2, Caiming Xiong2, Shafiq Joty2, Aws Albarghouthi1, Frederic Sala1
1University of Wisconsin-Madison, 2Salesforce AI Research
arXiv Paper

🤗

 Model & Dataset
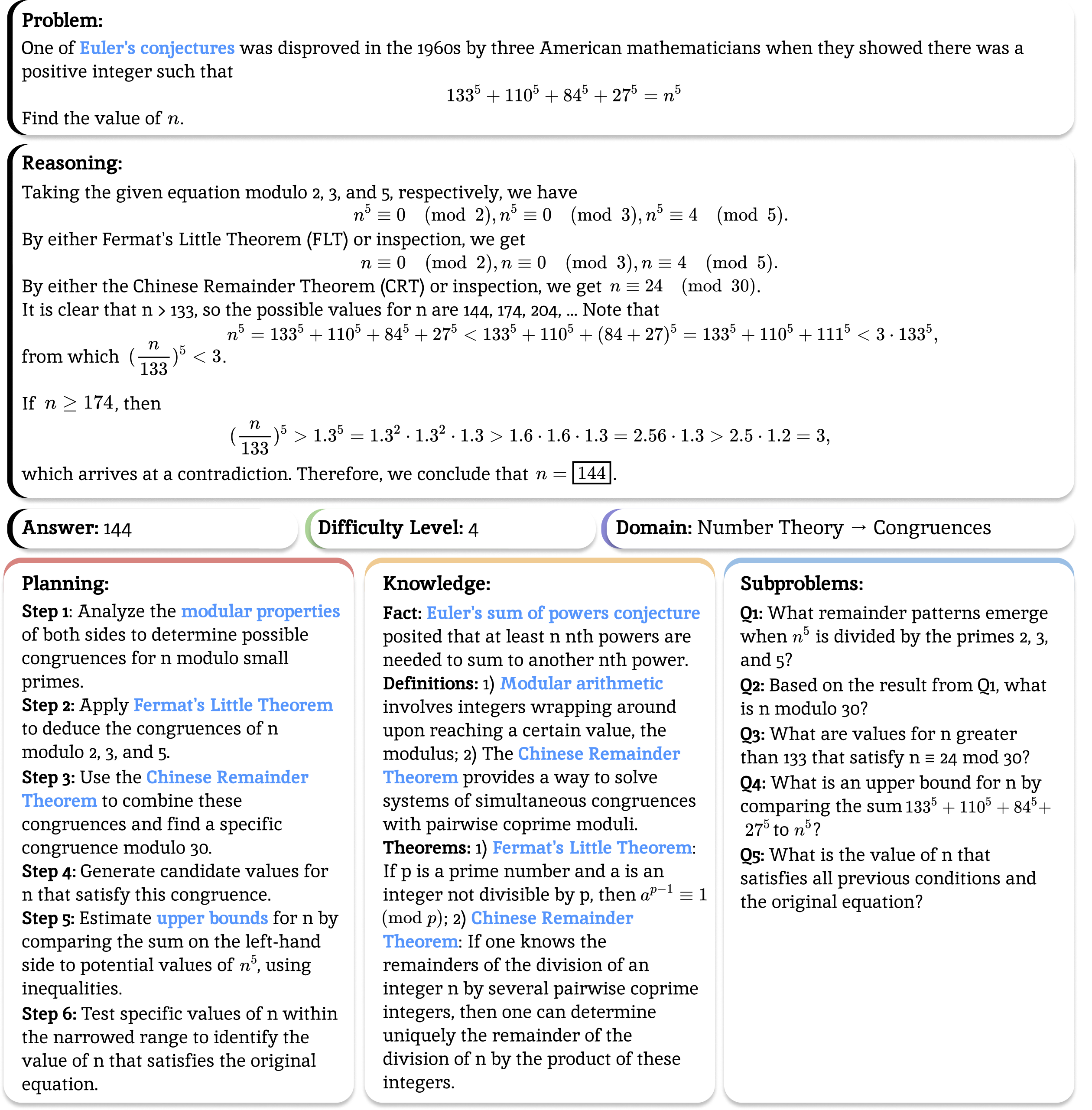
SPARKLE Framework Overview

SPARKLE is a fine-grained framework for evaluating LLM reasoning improvements under RL, analyzing models along three key axes: plan-following and execution, knowledge utilization, and subproblem decomposition. The benchmark includes annotated planning skeletons, curated knowledge, and decomposed subproblems to systematically study these capabilities and the impact of problem difficulty.

Introduction

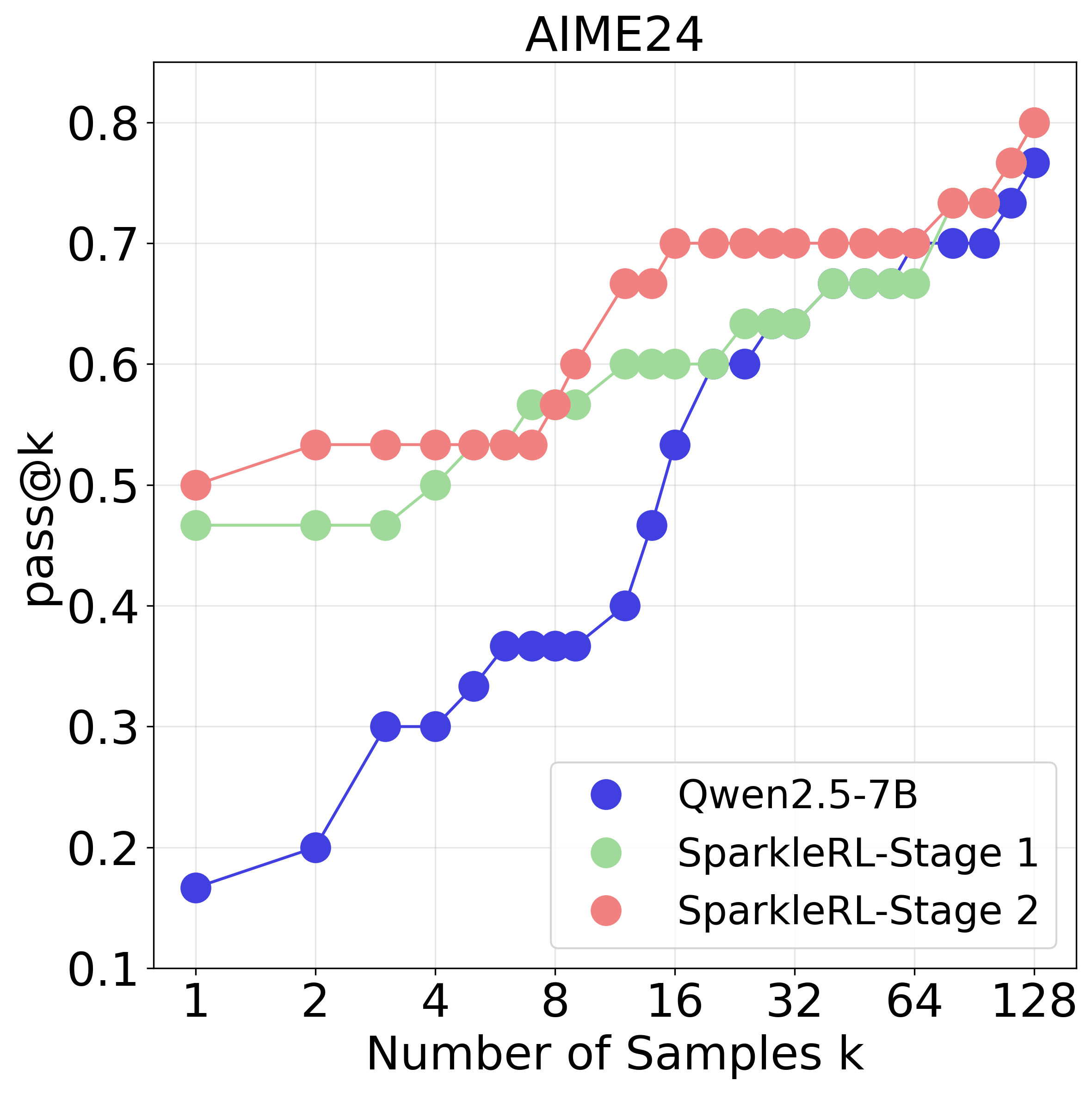
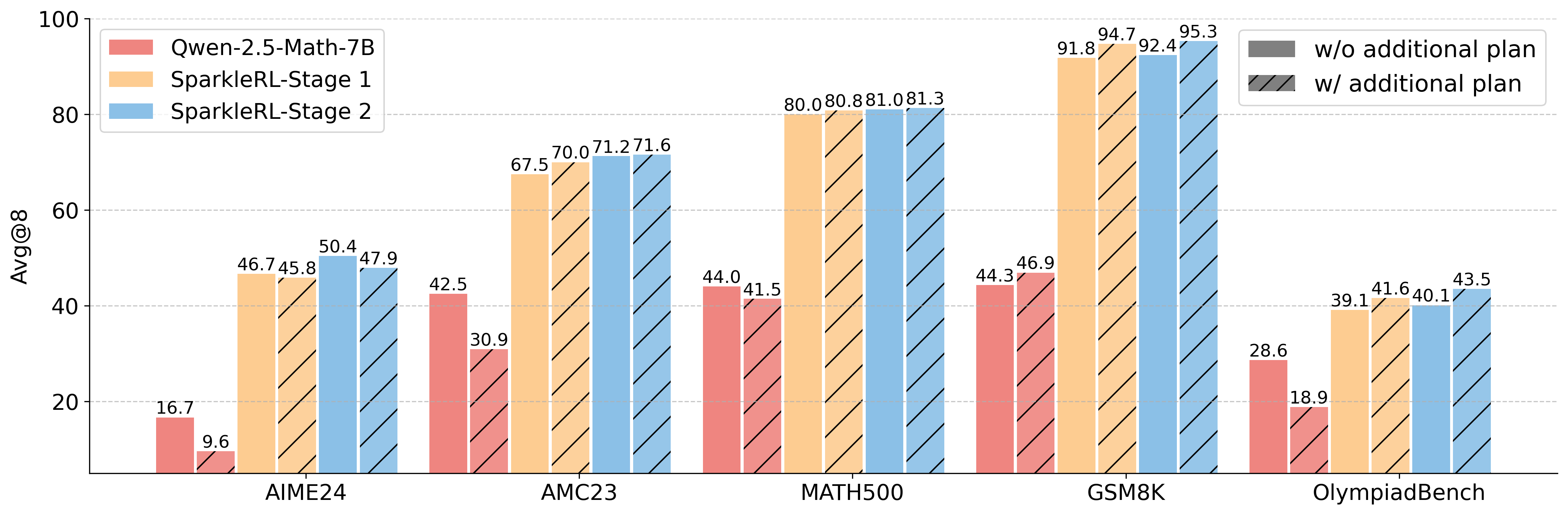
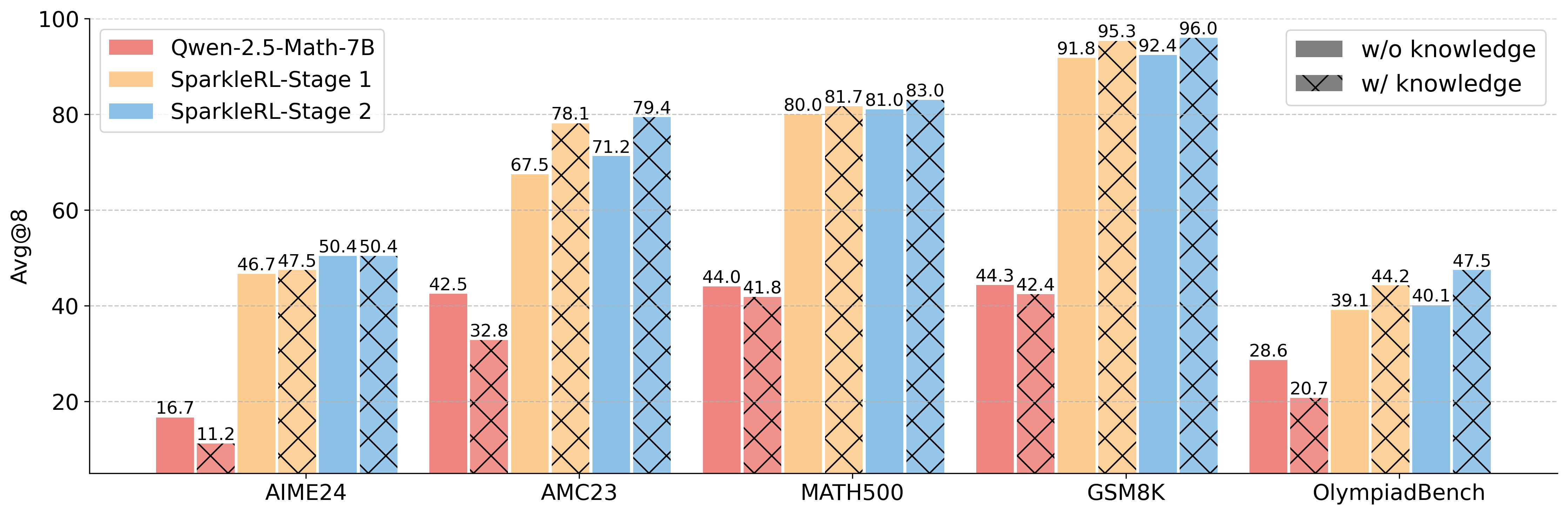
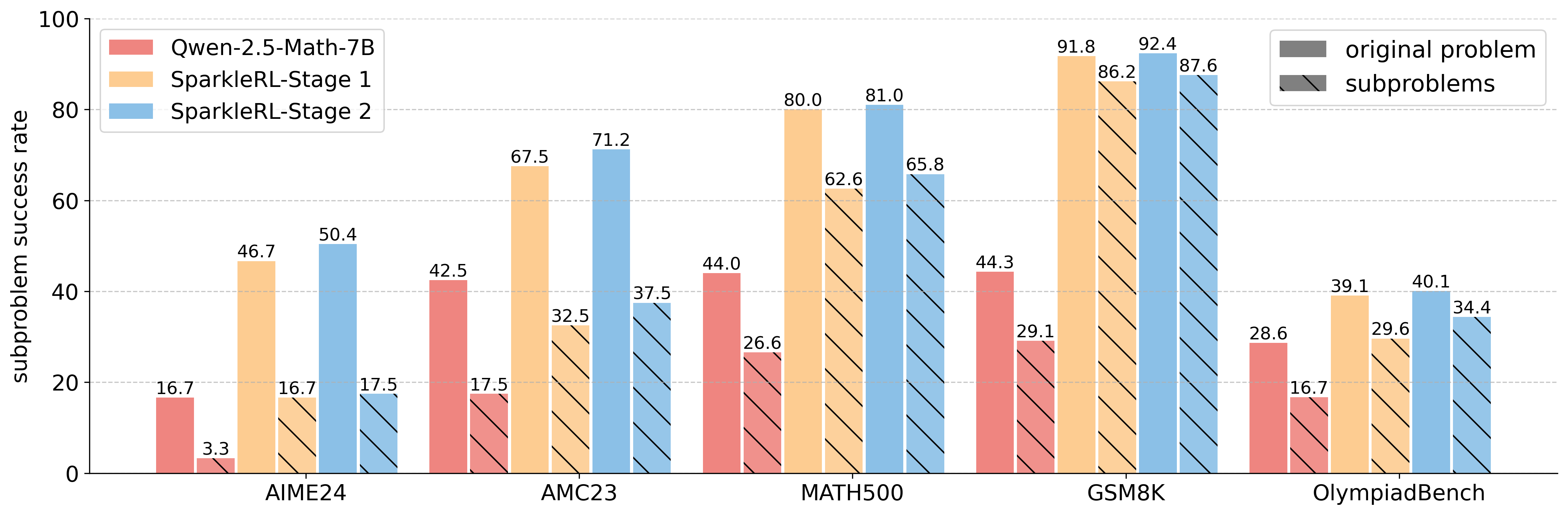
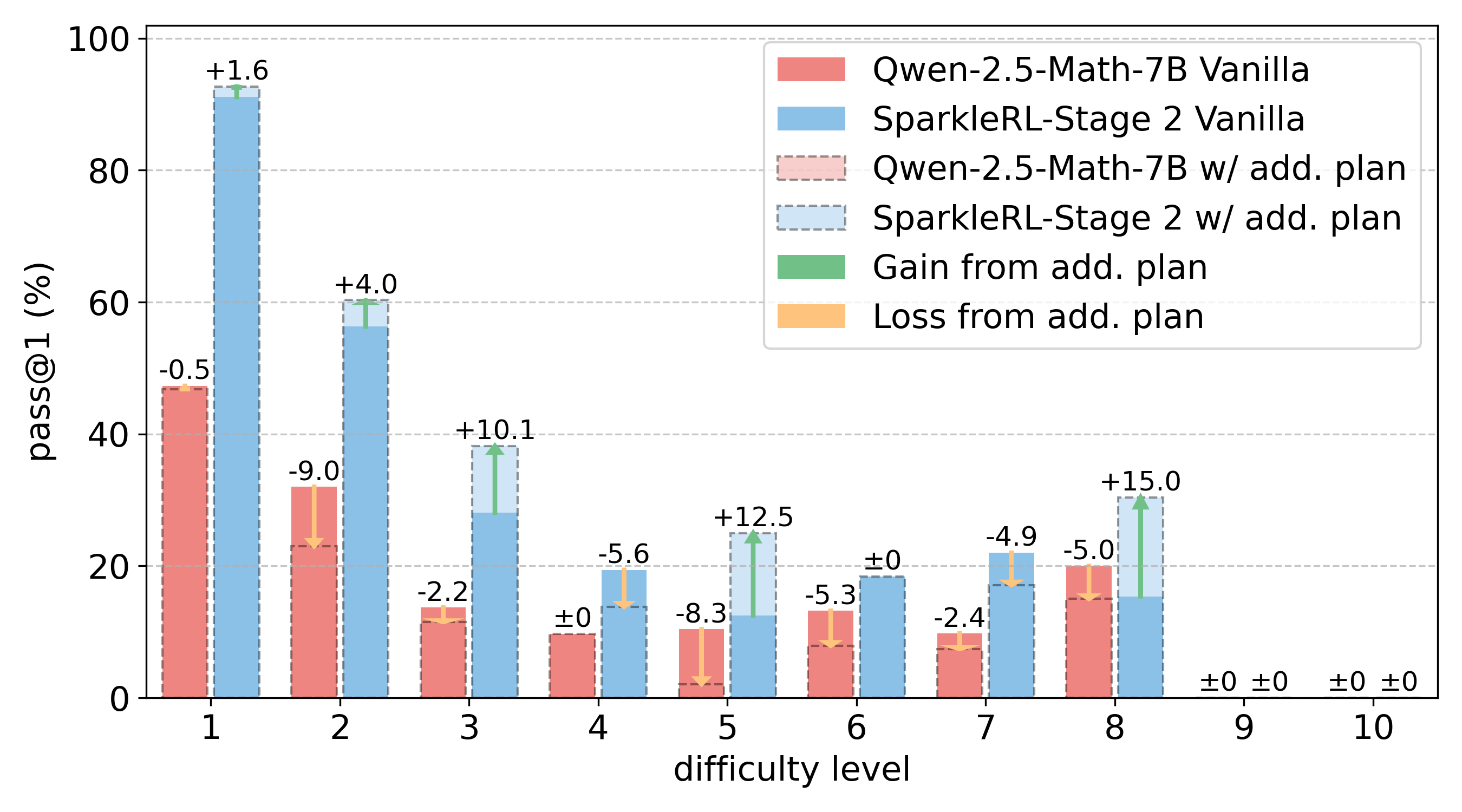
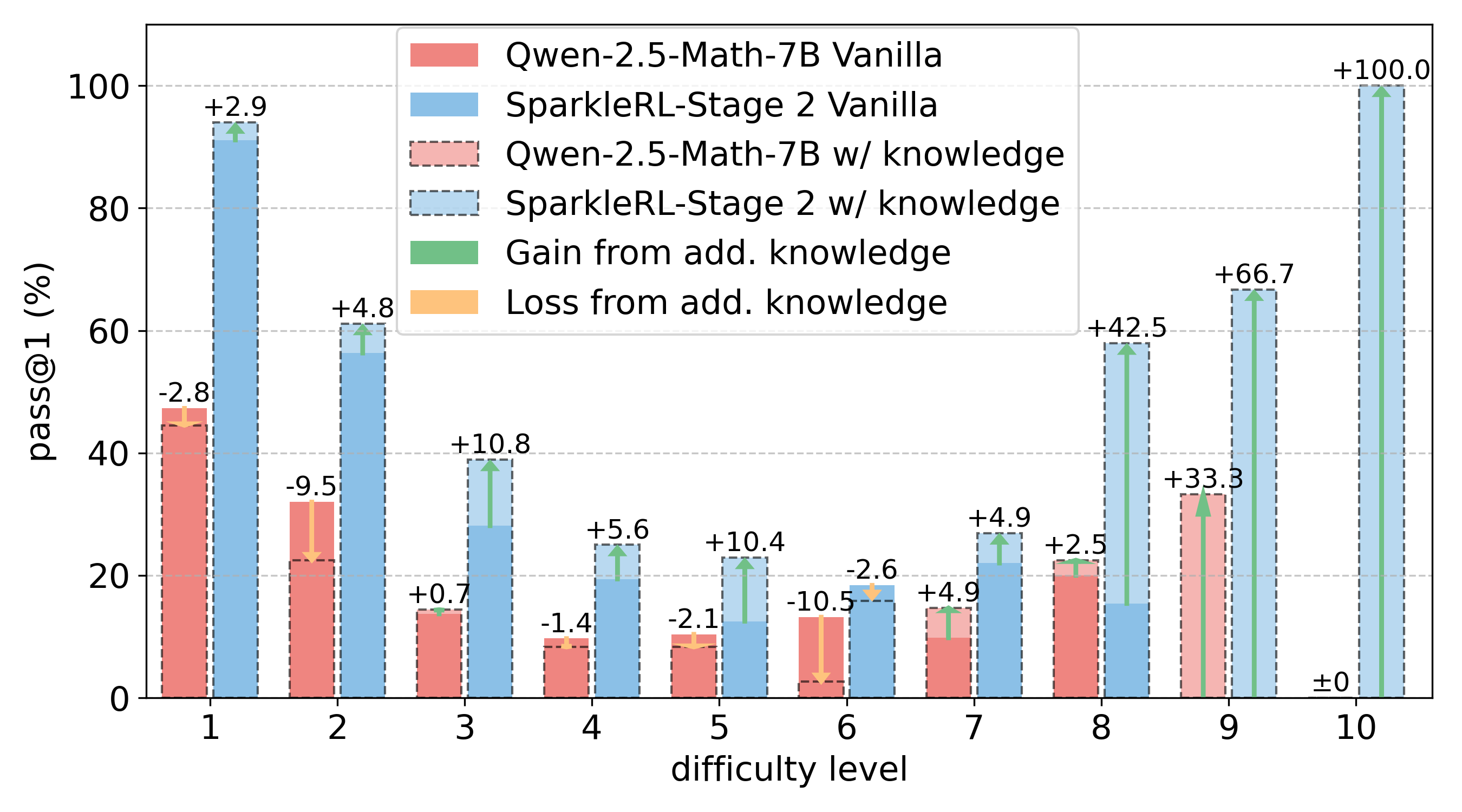
Reinforcement learning (RL) has become the dominant paradigm for endowing language models with advanced reasoning capabilities. Despite the substantial empirical gains demonstrated by RL-based training methods like GRPO, a granular understanding of their advantages is still lacking. To address this gap, we introduce a fine-grained analytic framework to dissect the impact of RL on reasoning. Our framework specifically investigates key elements that have been hypothesized to benefit from RL training: (1) plan-following and execution, (2) problem decomposition, and (3) improved reasoning and knowledge utilization. Using this framework, we gain insights beyond mere accuracy. For instance, providing models with explicit step-by-step plans surprisingly degrades performance on the most challenging benchmarks, yet RL-tuned models exhibit greater robustness, experiencing markedly smaller performance drops than their base counterparts. This suggests that RL may not primarily enhance the execution of external plans but rather empower models to formulate and follow internal strategies better suited to their reasoning processes. Conversely, we observe that RL enhances the model's capacity to integrate provided knowledge into its reasoning process, leading to performance improvements across diverse tasks. We also study difficulty, showing improved training by developing new ways to exploit hard problems. Our findings lay a foundation for more principled training and evaluation of reasoning models.

Key Takeaways

💡 Insight 1: Hard problems remain valuable when appropriately structured by augmenting problems with partial solutions during RL training.

ModelAIMEAMCMATH500GSM8KOlympiadAvg.
Qwen-2.5-Math-7B-Base16.6742.5044.0342.5328.6535.23
SparkleRL-Stage 146.67 (↑30.00)67.50 (↑25.00)80.00 (↑35.97)91.77 (↑49.24)39.11 (↑10.46)65.01
SparkleRL-Stage 2 (Hard)41.67 (↑25.00)65.94 (↑23.44)80.50 (↑36.47)92.45 (↑49.92)37.39 (↑8.74)63.59
SparkleRL-Stage 2 (Mix)40.00 (↑23.33)63.44 (↑20.94)80.78 (↑36.75)92.52 (↑49.99)38.85 (↑10.20)63.12
SparkleRL-Stage 2 (Aug)50.42 (↑33.75)71.25 (↑28.75)81.00 (↑36.97)92.38 (↑49.85)40.11 (↑11.46)67.03

Table: Avg@8 performance across benchmarks. Best results bolded; red deltas show absolute gain over base. Stage 1 trains on the full dataset. Stage 2 explores problem difficulty via three strategies: using only hard problems, mixing difficulties, or augmenting hard problems with partial solutions.

💡 Insight 2: RL improves sample efficiency.

💡 Insight 3: RL-tuned models are more flexible in plan execution—often outperforming human-authored plans with their own strategies.

💡 Insight 4: RL improves knowledge integration, unlike base models which degrade when given additional info.

💡 Insight 5: RL-tuned models still struggle with subproblem resolution, despite success on whole problems.

💡 Insight 6: As difficulty increases, knowledge boosts RL-tuned models more than planning does.

BibTeX

@misc{wang2025sparkle,
        title={Beyond Accuracy: Dissecting Mathematical Reasoning for LLMs Under Reinforcement Learning}, 
        author={Jiayu Wang and Yifei Ming and Zixuan Ke and Caiming Xiong and Shafiq Joty and Aws Albarghouthi and Frederic Sala},
        year={2025},
        eprint={2506.04723},
        archivePrefix={arXiv},
        primaryClass={cs.AI},
        url={https://arxiv.org/abs/2506.04723}, 
  }